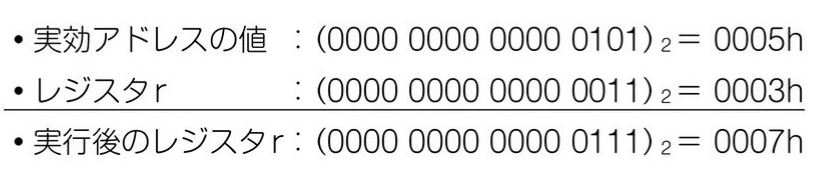機械語と進数¶
はじめに¶
本サイトにつきまして、以下をご認識のほど宜しくお願いいたします。
01. 機械語と2進数の関係¶
機械語とは¶
あらゆる情報を『0』と『1』の2進数を機械語として、CPUに対して、命令が実行される。
さまざまな進数とbitの関係¶
しかし、人間が扱ううえでは 8 進数あるいは 16 進数に変換して表すことが適している。
2 進数1ケタが『1bit』と定義されている。
8 進数の1ケタは 2 進数の3ケタ (=3bit) に相当し、16 進数の1ケタは 2 進数の4ケタ (4bit) に相当する。
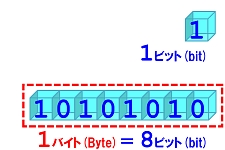
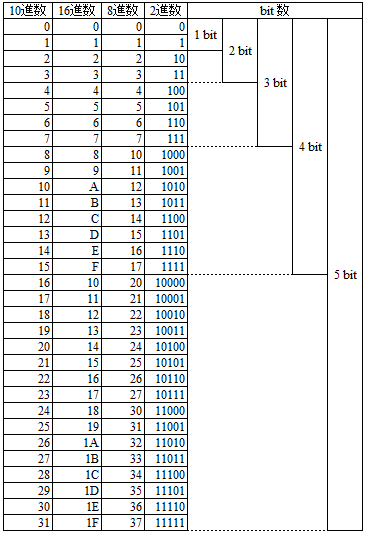
なぜ8bitを1Byteとするのか? (半角英数字とbitの関係)¶
8bitを一区切りとして、1Byteと表す。
これは、半角英数字一文字が8bitのデータサイズを持つからである。
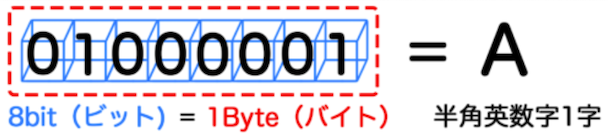
Byte単位¶
1000 Byte = 1k Byte
一般的なCPUが扱える情報の種数¶
CPUでは、各データは2進法によって区別されている。CPUは4 、8、16、32-bitバージョンと進歩し、2008年の後半からは 64-bitバージョンのCPUが普及し始めた。1-bitは2種類の情報を表せるため、32-bitのCPUでは2^32、64-bitでは2^64の種類の情報を扱える。
01-02. 機械語命令の種類¶
設定命令¶
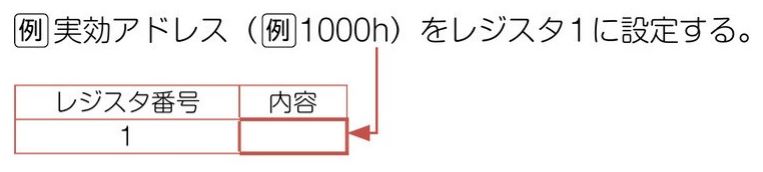
▼ 実行アドレスをレジスタに設定する場合¶
▼ 実行アドレスが指す語の内容をレジスタに設定する場合¶
▼ レジスタの内容を実行アドレスに格納する場合¶
シフト命令¶
計算命令¶
レジスタから取り出した値を別の値と足し、その結果を元のレジスタに設定すること。
論理演算命令¶
01-03. シフト命令¶
論理左シフト¶
最上位に正負を表す『符号bit』を設定せずに、シフトを実行する。
2進数の場合…
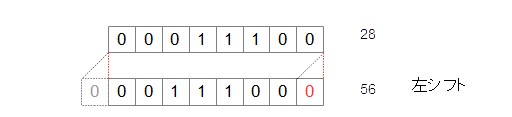
左に 1bitシフトすると『2倍』
左に 1bitシフトし、元の値を足すを『3倍』
左に 2bitシフトすると『4倍』
左に 2bitシフトし、元の値を足すと『5倍』
左に 2bitシフトし、元の値を足して『5倍』。
加えて 2bitシフトすると『10倍』
左に 3bitシフトすると『8倍』
▼ 正の数の場合¶
*例*
00011100
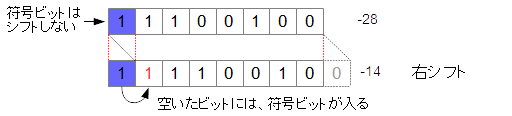
▼ 負の数の場合¶
*例*
11100100
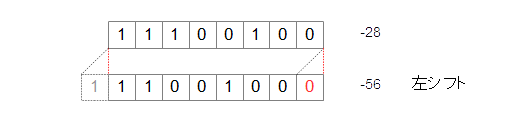
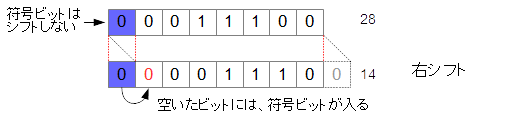
論理右シフト¶
最上位に正負を表す『符号bit』を設定せずに、シフトを実行する。
2進数の場合…
右に 1bitシフトすると『1/2』
右に 2bitシフトすると『1/4』
右に 3bitシフトすると『1/8』
▼ 正の数の場合¶
*例*
00011100
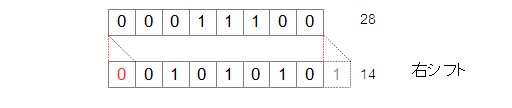
▼ 負の数の場合 (計算はできない)¶
*例*
11100100
負の数で論理右シフトを実行する場合、間違った計算が行われてしまう。
こういう場合、算術シフトが使用される。

算術左シフト¶
最上位に正負を表す『符号bit』を設定し、シフトを実行する。
2進数の場合…
左に 1bitシフトすると『2倍』
左に 1bitシフトし、元の値を足すを『3倍』
左に 2bitシフトすると『4倍』
左に 2bitシフトし、元の値を足すと『5倍』
左に 2bitシフトし、元の値を足して『5倍』。
加えて 2bitシフトすると『10倍』
左に 3bitシフトすると『8倍』
▼ 正の数の場合¶
*例*
00011100
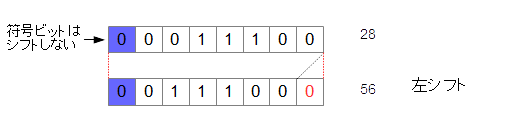
▼ 負の数の場合¶
*例*
00011100
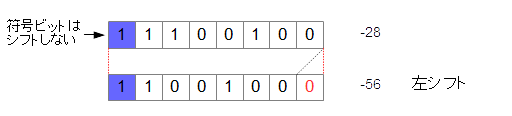
算術右シフト¶
2進数の場合…
最上位に正負を表す『符号bit』を設定し、シフトを実行する。
右に 1bitシフトすると『1/2』
右に 2bitシフトすると『1/4』
右に 3bitシフトすると『1/8』
▼ 正の数の場合¶
*例*
00011100
▼ 負の数の場合¶
01-04. 機械語命令の実行手順¶
実行手順¶
(1)-
16進数が2進数に変換され、記号へ値が割り当てられる。 (ビット分割)
(2)-
記号の値を基に、実行アドレスの計算方法が選択され、実行される。 (実行アドレスの計算)
(3)-
実行アドレスを基に、機械語命令が実行され、値がレジスタやメモリに書き留められる。 (機械語命令のトレース)
(1)¶
- ビット分割
*例*
命令:20B3h
▼ 16進数の2進数への変換¶
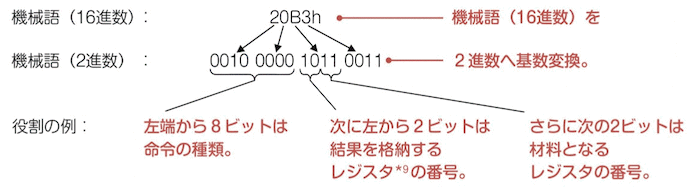
▼ 記号への値の割り当て¶
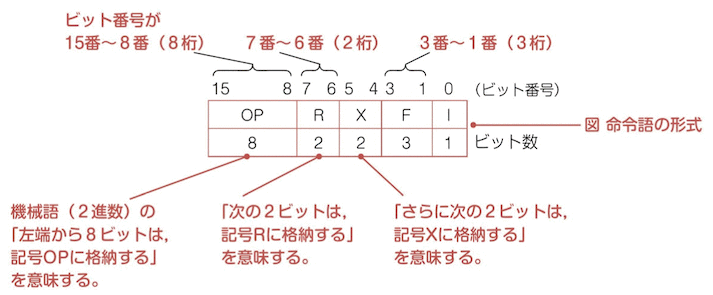
(2)¶
- 実効アドレスの計算
▼ 実行アドレスの計算方法の選択¶
『X=2』、『I = 1』より、表の網掛けの計算式を選択。
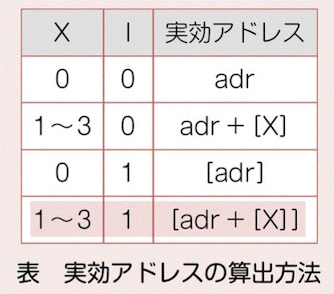
▼ 実効アドレスの計算の実行¶
ここに、レジスタ番号と内容の表を張る。
(実効アドレス) = [adr + [X] ]
= [1000h + [レジスタ2] ] (※配列のように、レジスタ2の値を参照)
= [1000h + 0002h]
= [1002h]
= 1003h
(3)¶
- 機械語命令のトレース
01-05. 構文解析における数式の認識方法¶
逆ポーランド表記法 (後置表記法)¶
演算子 (例:+、-、×、÷ など) を被演算子 (数値や変数、また計算の結果) の後ろに書くことにより、数式を表す方法。
補足として、人間が使用している表記方法は、『中置記法』という。
*例*
Y = ( A + B ) × ( C - ( D ÷ E ) )
(1)-
括弧は先に計算するので塊と見なす。
( A + B ) ⇒ AB+
(2)-
括弧は先に計算するので塊と見なす。
( D ÷ E ) ⇒ DE ÷
(3)-
括弧は先に計算するので塊と見なす。
( AB + ) × ( C - DE ÷ ) ⇒ (AB +) (CDE÷-) ×
(4)-
括弧を外しても、塊はそのまま。
(AB+) (CDE÷-) × ⇒ AB+CDE÷-×
(5)-
左辺と右辺をそれぞれ塊と見なす。
Y = AB+CDE÷-× ⇒ YAB+CDE÷-×=
01-06. CPUにおける小数の処理方法¶
固定小数点数¶
『この位置に小数点がある』な前提で数字を扱うことによって、小数点を含む数値を表す方法。
CPUは、数値に対し、特定の位置に小数点を打つ。
浮動小数点数¶
指数表記を使用することによって、小数点を含む数値を表す方法。
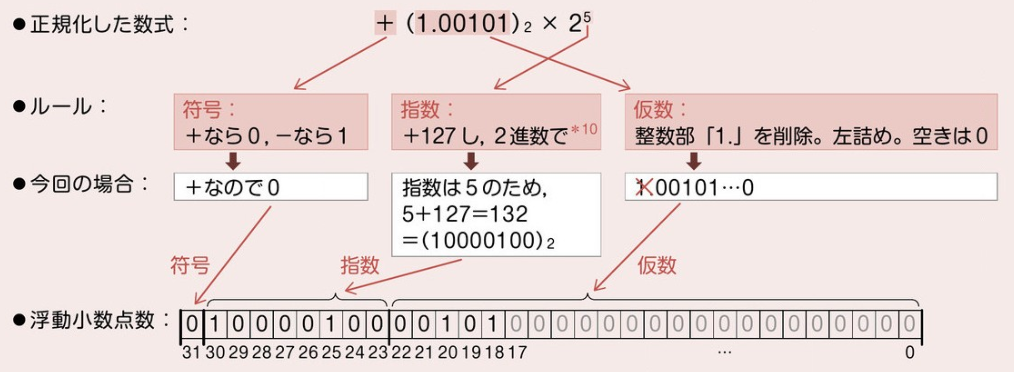
▼ 正規化した数式から浮動小数点数への変換¶
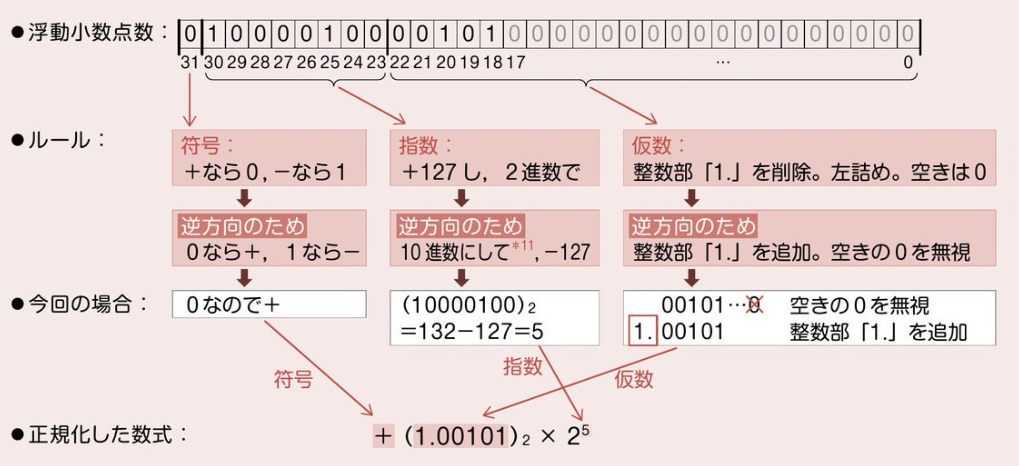
▼ 浮動小数点数から正規化した数式への変換¶
指数部と仮数部を調節し、できるだけ仮数部の上位桁へ0が入らないようにして、誤差を少なくすること。例えば、ある計算の結果が 0.012345×10^-3 だった場合、仮数部を0.1~1の範囲に収めるため、0.12345×10^-4 に変更する。
01-07. 誤差¶
『誤差』:実際の数値とCPUが表現できる数値の間に生じるズレのこと。
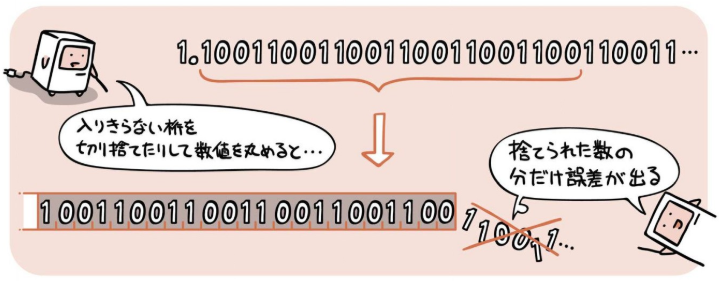
無限小数¶
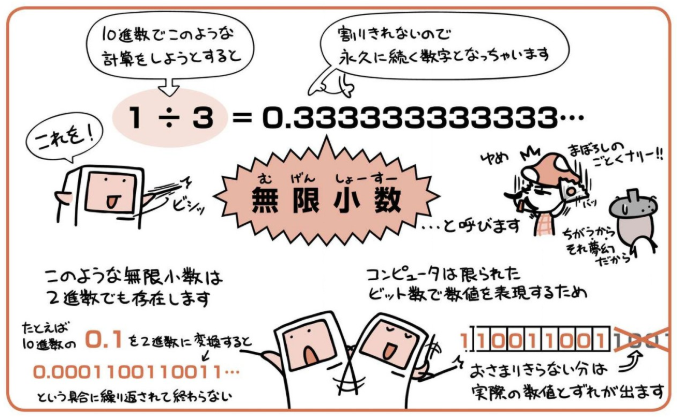
桁溢れ誤差¶
*例*
初代ドラクエ
初代のドラゴンクエストの経験値の上限は『65535』だった。
これは、経験値が16bit (2 Byte) で表されており、桁溢れが起きることを防ぐために 65535 以上は計算しないようになっていた。
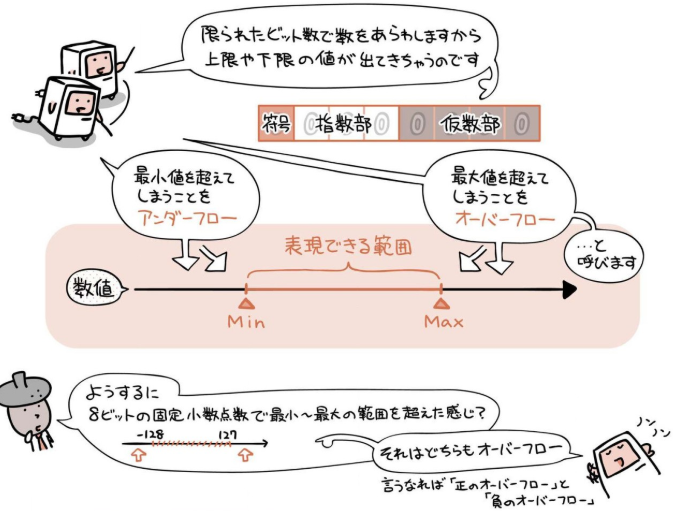
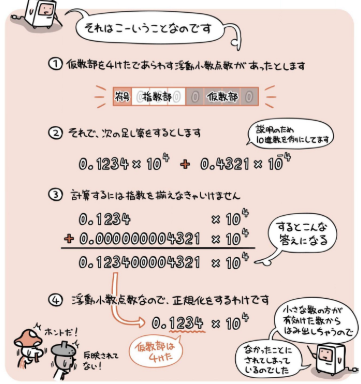
情報落ち¶
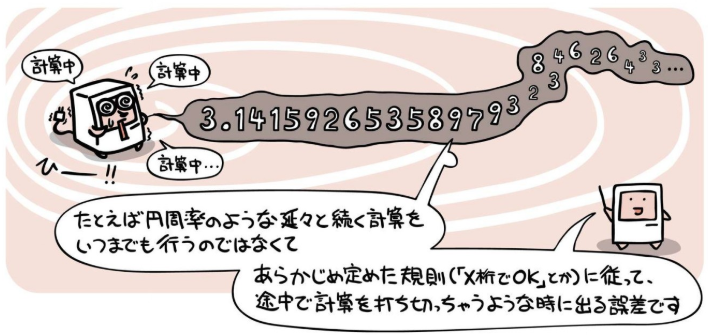
打切り誤差¶
円周率は、途中で計算を打ち切る。
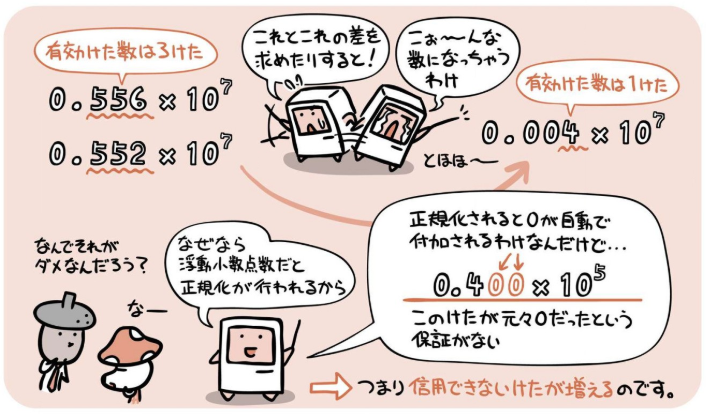
桁落ち¶
丸め誤差¶
02. N 進数 ➔ 10進数 (重み掛けを実行する)¶
16進数 ➔ 10進数¶
▼ 整数¶
*例*『CA125』
(1)-
『
(16^0 × 5) + (16^1 × 2) + (16^2 × 1) + (16^3 × A) + (16^4 × C)』というように、下の位から、順に16^Nをかけていく。 (AとCは、10進数に変換して『10』と『12』) (2)-
(1×5) + (16×2) + (256×1) + (4096×10) + (65536×12) = 827685
▼ 少数¶
2進数 ➔ 10進数¶
▼ 整数¶
『1101101』
(1)-
『
(2^0 × 1) + (2^1 × 0) + (2^2 × 1) + (2^3 × 1) + (2^4 × 0) + (2^5 × 1) + (2^6 × 1)』というように、下の位から、順に2^Nをかけていく。
▼ 少数¶
02-02. 10進数 ➔ N 進数 (Nで割り続ける)¶
10進数 ➔ 16進数¶
▼ 整数¶
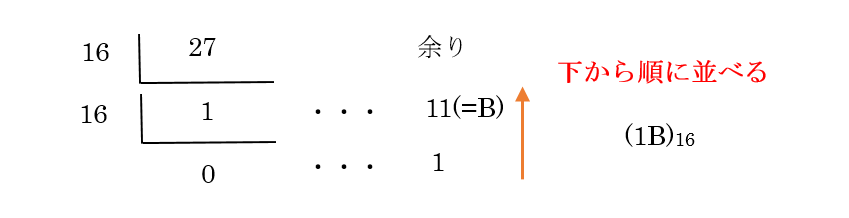
*例*『27』
(1)-
27を16で割り続ける。 (2)-
16進数で10~15は、A~Fで表記されるため、
11をBで表記。 (3)-
余りを並べ、答えは『1B』
▼ 少数¶
*例*『0.1015625』
(1)-
『
0.1015625』に16をかけ、整数部分を取り出す。 (0.1015625 × 16 = 1.625。『1』を取り出し、16進数に変換して『1』) (2)-
計算結果の少数部分に16を加えてかける。少数部分が0になるまで、これを繰り返す。 (
0.625 × 16 = 10.0より、『10』を取り出し、16進数に変換して『A』) (3)-
少数部分が0になったため、取り出した数を順に並べ、答えは『0.1A』
10進数 ➔ 2進数¶
▼ 整数¶
*例*『109』

▼ 少数¶
02-03. X 進数 ➔ 10進数 ➔ Y 進数¶
一度、10進数に変換してから、任意の進数に変換する。
16進数 ➔ 2進数¶
▼ 整数¶
*例*『20B3』
(1)-
2、0、B、3を10進数に変換して、『
(16^0 × 3) + (16^1 × 11) + (16^2 × 0) + (16^3 × 2) = 8371』 (2)-
10と15を2進数に変換して、『
0010』、『0000』、『1011』、『0011』 (3)-
よって、AFは10進法に変換して『
0010000010110011』
02-04. X 進数 ➔ 10 進数 ➔ Y 進数 ➔ 10 進数¶
16進数 ➔ 2進数¶
▼ 少数¶
*例*
2A.4C
(1)-
整数部分の
2Aを10進数に変換して、 (2)-
42を2進数に変換して、『
101010』。また、余り計算の時、余り1を2^Nに直しておく。 (3)-
整数の場合、下位の桁から、『
(2^0 × 0) + (2^1 × 1) + (2^2 × 0) + (2^3 × 1) + (2^4 × 0) + (2^5 × 1) + (2^6 × 0) + (2^7 × 0) + (2^8 × 0)』
=『2^5+2^3+2^1』
(※16進数からの変換の場合、101010は、00101010として扱うことに注意)
(4)-
76を2進数に変換して、『1001100』。また、余り計算の時、余り1を2^Nに直しておく。
(5)-
少数部分の場合、上位の桁から、『
(2^-1 × 0) + (2^-2 × 1) + (2^-3 × 0) + (2^-4 × 0) + (2^-5 × 1) + (2^-6 × 1) + (2^-7 × 0) + (2^-8 × 0)』
=『2^-2+2^-5+2^-6』
(※16進数からの変換の場合、1001100は、01001100として扱うことに注意)
(6)-
したがって、『
2^5+2^3+2^1+2^-2+2^-5+2^-6』
03. 論理回路¶
論理式¶

以下のベン図では、集合Aと集合Bは入力が『1』の場合、外側は入力が『0』の場合を表している。
演算方法を思い出すときには、ベン図を思い出せ。
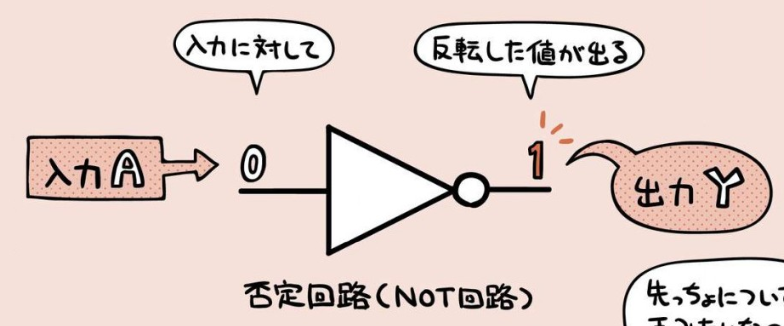
否定回路 (NOT回路) 、NOT演算、ベン図¶
丸い記号が否定を表す。

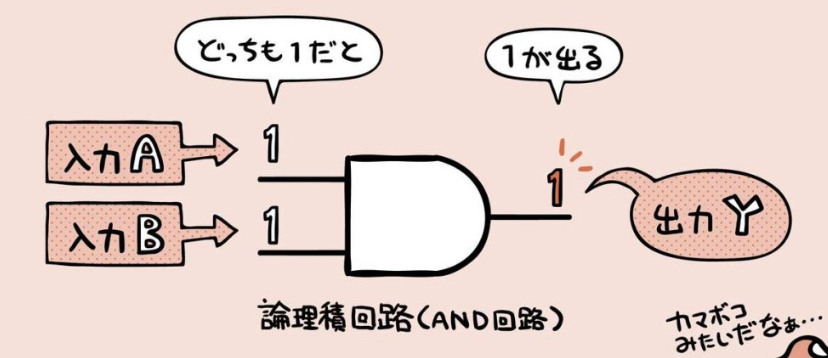
論理積回路 (AND回路) 、AND演算、ベン図¶
2 個のbitを比較して、どちらも『1』なら『1』を出力。

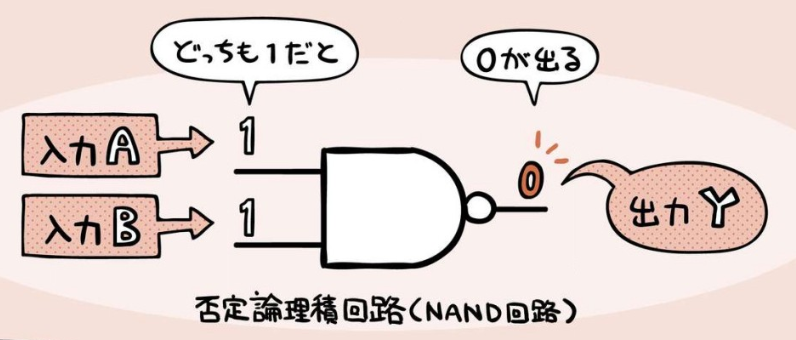
否定論理積回路 (NAND回路) 、NAND演算、ベン図¶
2 個のbitを比較して、どちらも『1』なら『0』を出力。
ベン図では両方が『1』以外の場合を指しているが、回路の出力をうまく説明できない…。

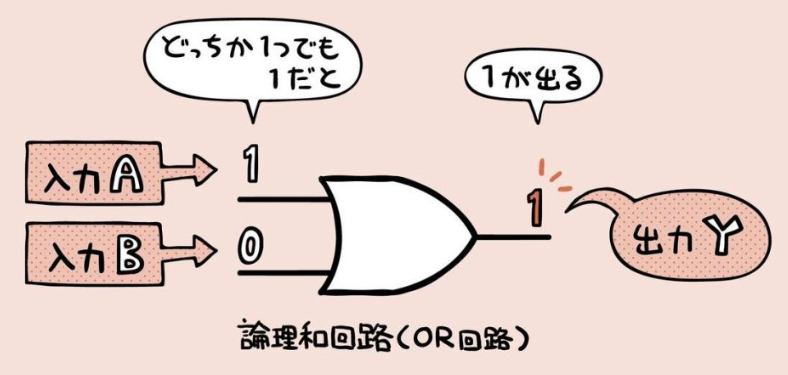
論理和回路 (OR回路) 、OR演算、ベン図¶
2 個のbitを比較して、どちらかが『1』なら『1』を出力。

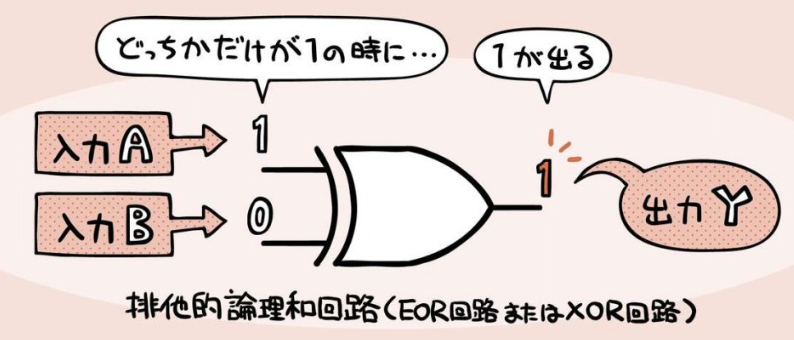
排他的論理和回路 (EOR回路/XOR回路) 、EOR演算、ベン図¶
2 個のbitを比較して、どちらかだけが『1』なら『1』を出力。

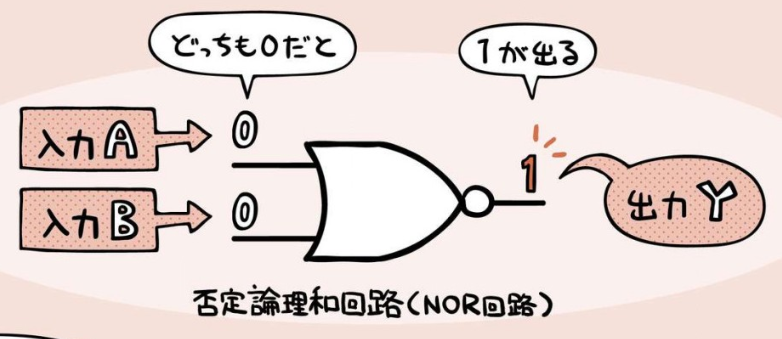
否定論理和回路 (NOR回路) 、NOR演算、ベン図¶
2 個のbitを比較して、どちらも『0』なら『1』を出力。

フリップフロップ回路¶
わかりやすい動画解説:https://www.youtube.com/watch?v=4vAGaWyGanU
SRAMの電子回路に使用している (6章を参照) 。
Set側に初期値『1』が入力される。
入力を『0』に変えても、両方の出力結果は変わらず、安定している。
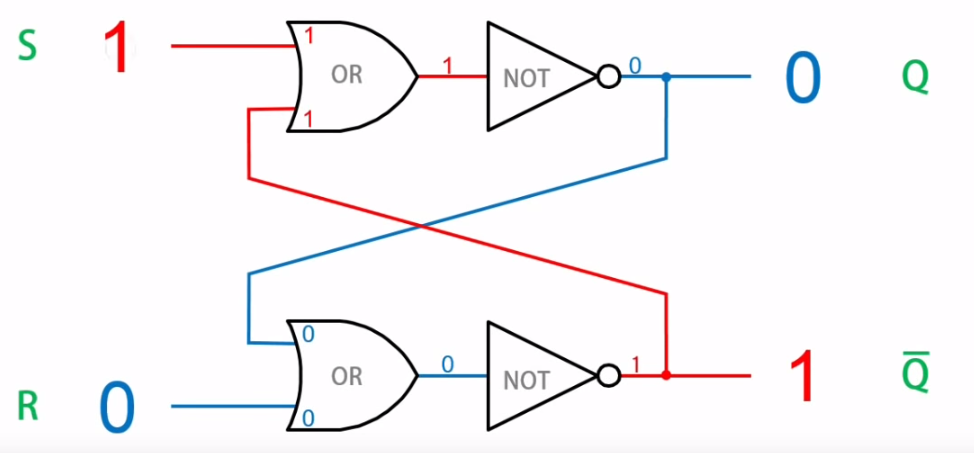
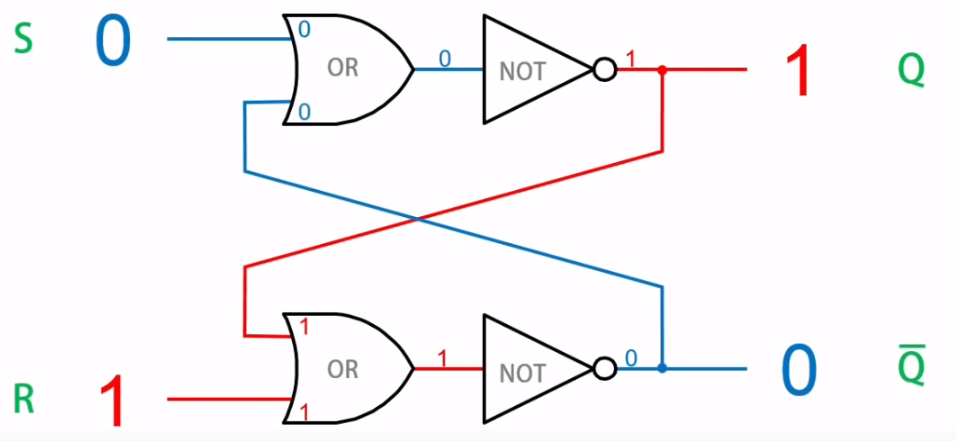
Reset側に『1』を入力すると、両方の出力結果は変化する。
03-02. 論理演算命令¶
論理積¶
*例題*
16進数の『F』は、2進数で『0000 0000 0000 1111』で表す。
よって、000Fを使用してAND演算した場合、下位4桁を変化させずに取り出せる。
1100 1101 1111 1000
0000 0000 0000 1111
ーーーーーーーーーーー
0000 0000 0000 1000
*例題*
16進数の『7F』は、2進数で『0000 0000 0111 1111』で表す。
よって、7Fを使用してAND演算した場合、下位7桁を変化させずに取り出せる。
1100 1101 1111 1000
0000 0000 0111 1111
ーーーーーーーーーーー
0000 0000 0111 1000
*例題*
否定論理積¶
論理和¶
排他的論理和¶
否定論理和¶
*例題*
XとYの否定論理積 X NAND Yは、NOT(X AND Y)として定義される。
X OR YをNANDのみを使用して表した論理式はどれか。
X=0、Y=0 の時にX OR Yが『0』になることから、『0』になる選択肢を探す。
▼ ((X NAND Y) NAND X) NAND Y¶
((0 NAND 0)NAND 0)NAND 0
=(1 NAND 0) NAND 0
=1 NAND 0
=1
▼ (X NAND X) NAND (Y NAND Y)¶
(0 NAND 0)NAND(0 NAND 0)
=1 NAND 1
=0
▼ (X NAND Y) NAND (X NAND Y)¶
(0 NAND 0)NAND(0 NAND 0)
=1 NAND 1
=0
▼ X NAND (Y NAND (X NAND Y))¶
0 NAND(0 NAND(0 NAND 0))
=0 NAND (0 NAND 1)
=0 NAND 1
=1