統計分析@R¶
はじめに¶
本サイトにつきまして、以下をご認識のほど宜しくお願いいたします。
データ分析で気をつけること¶
(1)-
データ分析によって、何を明らかにしたいのか。
(2)-
明らかにすることのために、どのデータ分析が必要なのか。
(3)-
必要なデータ分析のために、どんな形式のデータを用意する必要があるのか。
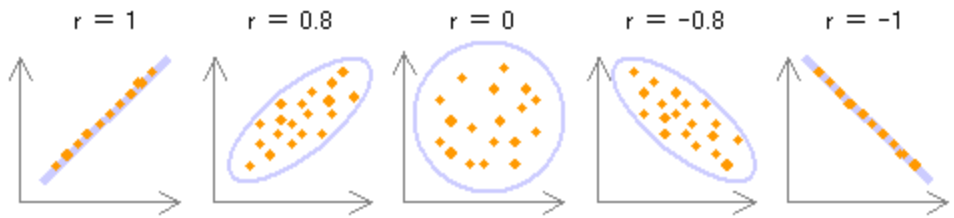
01. 相関分析¶
データに、どの程度の直線的関係があるかを検出する分析手法。
回帰分析を実行するか否かの判断材料になる。
*実装例*
# データを読み込む。
sample <- read.table("sample_edit.txt", header = T)
# 純広告とCV_純広告の散布図を作成。
g <- ggplot(sample, aes(x = 純広告, y = CV_純広告))
g <- g + geom_point()
plot(g)
# 純広告とCV_純広告の相関分析を実行する。
ts<-ts(sample[,2:5])
cor(ts, method = "pearson")
# 分析結果
# 純広告 リスティング CV_純広告 CV_リスティング
# 純広告 1.00000000 0.5247992 0.1065025 -0.09415535
# リスティング 0.52479919 1.0000000 -0.2360605 0.20821230
# CV_純広告 0.10650249 -0.2360605 1.0000000 0.19500011
# CV_リスティング -0.09415535 0.2082123 0.1950001 1.00000000
# // 純広告とCV_純広告の間には、弱い直線的関係がある。
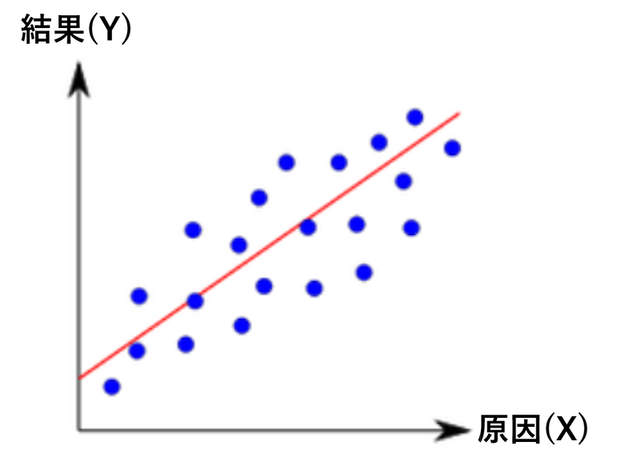
02. 線形回帰分析¶
因果関係がありそうなデータに対して、横軸を原因、また縦軸を結果とし、もっとも当てはまりの良い線形モデルを推定する分析手法。
モデルの精度が高ければ因果関係の証明になり、またモデルに原因を代入することにより結果を予測できる。
単回帰分析¶
原因と結果が1つずつと仮定したときに、もっとも当てはまりの良い線形モデルを推定できる。
▼ 回帰方程式¶
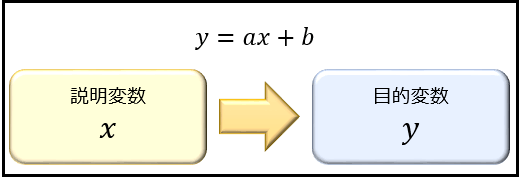
*実装例*
# データを読み込む。
sample <- read.table("sample_edit.txt", header = T)
ts <- ts(sample[,2:5])
# データ型を変更。
df <- data.frame(ts)
# CV_純広告と純広告に基づく線形回帰分析を実行する。
Reg <- lm(CV_純広告 ~ 純広告,df)
# 分析結果
summary(Reg)
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.099e+01 2.405e+00 4.571 3.11e-05 ***
# 純広告 2.239e-05 2.927e-05 0.765 0.448
# // 純広告の回帰係数のp値 > 0.05 より、因果関係がない可能性。
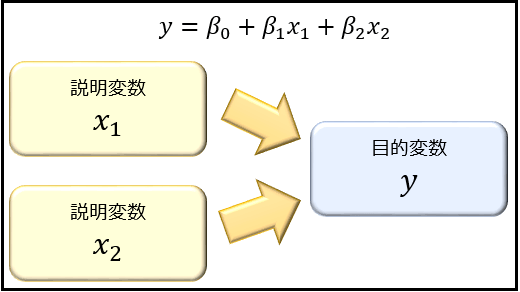
重回帰分析¶
原因が2つ以上で結果が1つと仮定したときに、もっとも当てはまりの良い線形モデルを推定できる。
ただし、グラフでは、モデルは平面で表す。
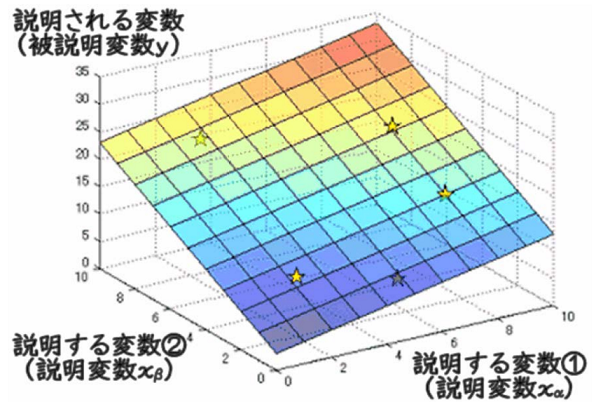
▼ 回帰方程式¶
*実装例*
# データを読み込む。
sample <- read.table("sample_edit.txt", header = T)
days <- weekdays(as.Date(sample$DATE))
sample1<-transform(sample,days=days)
library(caret)
# 曜日をダミー変数に変換
tmp <- dummyVars(~days, data=sample1)
days1 <- as.data.frame(predict(tmp, sample1))
# 曜日の順番を整形
days2 <- days1 [ c(3,1,4,7,2,5,6) ]
# 広告データと曜日データを結合
ts1 <- cbind(sample, days2)
# データ型を変更
df <- data.frame(ts1)
# 重回帰分析を実行する。
Reg<-lm(CV_純広告 ~ days.月曜日+days.火曜日+days.水曜日+days.木曜日+days.金曜日,df)
# 分析結果
summary(Reg)
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 8.857 1.007 8.797 1.69e-11 ***
# days.月曜日 5.286 1.744 3.031 0.003957 **
# days.火曜日 4.893 1.670 2.930 0.005212 **
# days.水曜日 6.143 1.670 3.679 0.000601 ***
# days.木曜日 5.893 1.670 3.529 0.000944 ***
# days.金曜日 4.393 1.670 2.631 0.011479 *
# // 月、水、金の回帰係数のp値 < 0.05 より、月水金で因果関係があり、火金で因果関係がない可能性。
02-02. 非線形回帰分析¶
因果関係がありそうなデータに対して、横軸を原因、また縦軸を結果とし、もっとも当てはまりの良い非線形モデルを推定する分析手法。
モデルの精度が高ければ因果関係の証明になり、またモデルに原因を代入することにより結果を予測できる。
非線形モデルを推定するためには、モデルを一般化し、一般化線形モデルとして処理する必要がある。
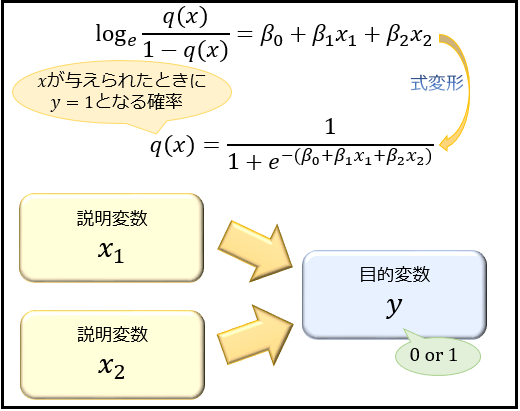
ロジスティック回帰分析¶
説明変数が質的変数の場合、もっとも当てはまりの良い非線形モデル (ロジスティック分布) を推定する。
▼ 回帰方程式¶
*実装例*
# データを読み込む。
sample<-read.csv("CV_data2.csv",header=T)
# リンク関数をロジットとし、非線形モデルを一般化する。
result_lg = glm(CP申込み ~ 性別+経済関連, sample, family=binomial)
# オッズ比を出力
exp(result_lg2$coefficients)
# オッズ比の出力結果
# (Intercept) 性別 経済関連
# 0.08930881 14.98017457 1.75649720
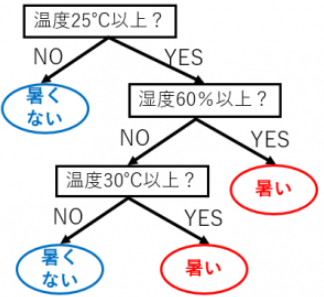
03. 決定木分析¶
データに対して、もっとも当てはまりの良い決定木モデルを推定する分析手法。
分類木分析¶
決定木モデルを分類モデルとして使用する場合の決定木分析。
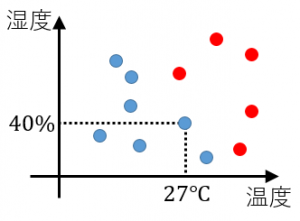
▼ 図解例¶
赤い点:被験者が暑いと感じた日
青い点:被験者が暑くないと感じた日

*実装例*
# データを読み込む。
sample <- read.csv("CV_data.csv", header = T)
# 識別値のidを説明変数から除いたうえで、決定木を作成。
library(rpart)
tree <- rpart(CV~AGE + SEX + AD, data = sample)
# partykitパッケージで決定木をグラフ化。
library(partykit)
plot(as.party(tree), tp_args = T)
# rattleとrpart.plotパッケージで決定木をグラフ化。
library(rattle)
library(rpart.plot)
fancyRpartPlot(tree)
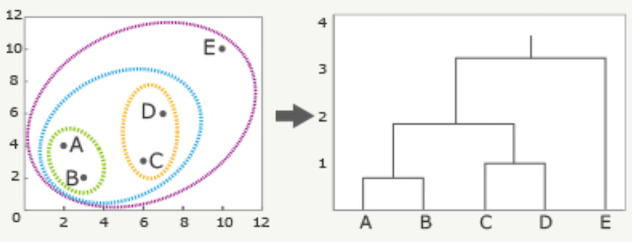
04. 階層クラスター分析¶
データを、似ている順に階層的にグループ化 (クラスタリング) していく分析手法。
データ間の同一性を明らかにできる。
*実装例*
# データを読み込む。
sample1 <- read.csv("CV_data.csv")
# ダミー変数に変換するために必要な情報が格納されたリストを作成。
library(caret)
tmp <- dummyVars(~., data = sample1)
# リストを基に、sample1の質的変数をダミー変数に変換。
sample1.dummy <- as.data.frame(predict(tmp, sample1))
# id以外の列を標準化。
scale.dummy <- scale(sample1.dummy[, 2:9])
# 距離行列を計算。
d1 <- dist(scale.dummy)
# ウォード法による階層クラスター分析を行い、グラフ化。
cluster1 <- hclust(d1, method = "ward.D2")
plot(cluster1)
05. グラフ作成関数¶
ggplot 関数¶

(1)-
ggplot関数:グラフのキャンバスを準備 (2)-
geom_XXX関数:グラフをプロット (3)-
theme関数:グラフを追加加工