アルゴリズムロジック@PHP¶
はじめに¶
本サイトにつきまして、以下をご認識のほど宜しくお願いいたします。
01. 並び替えのアルゴリズム¶
例えば、次のような表では、どのような仕組みで『昇順』『降順』への並び替えが行われるのだろうか。

基本選択法 (選択ソート)¶
▼ 最小選択法¶
*実装例*
(1)-
比較基準値を決める。
(2)-
最初の数値を比較基準値とし、
n個の中からもっとも小さい数字を探し、それと入れ替える。 (3)-
次に、残りの
n-1個の中からもっとも小さい数字を探し、それを2番目の数字と入れ替える。 (4)-
この処理を
n-1回繰り返す。
<?php
function minSelectSort(array $array): array
{
// 比較基準値を固定し、それ以外の数値と比べていく。
for($i = 0; $i < count($array)-1; $i++){
// 比較基準値を仮の最小値として定義。
$min = $array[$i];
// 比較基準値の位置を定義
$position = $i;
// 比較基準値の位置以降で、数値を固定し、順番に評価していく。
for($j = $position + 1; $j < count($array); $j++){
// 比較基準値の位置以降に小さい数値があれば、比較基準値と最小値を更新。
if($min > $array[$j]){
$position = $j;
$min = $array[$j];
}
}
// 比較基準値の位置が更新されていなかった場合、親のfor文から抜ける。
if($i == $position){
break;
}
// 親のfor文の最小値を更新。
$array[$i] = $min;
// 次に2番目を比較基準値とし、同じ処理を繰り返していく。
}
return $array;
}
<?php
// 実際に使用してみる。
$array = array(10,2,12,7,16,8,13)
$result = selectSort($array);
var_dump($result);
// 昇順に並び替えられている。
// 2, 7, 8, 10, 12, 13, 16
*アルゴリズム解説*
データ中の最小値を求め、次にそれを除いた部分の中から最小値を求める。
この操作を繰り返していく。






クイックソート¶
*実装例*
(1)-
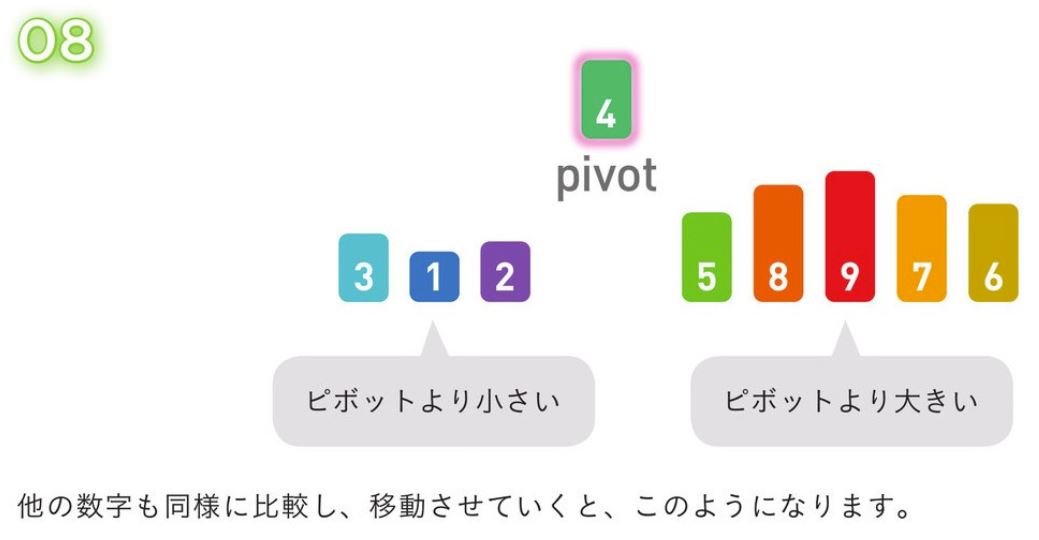
適当な値を基準値 (Pivot) とする (※できれば中央値が望ましい)
(2)-
Pivotより小さい数を前方、大きい数を後方に分割する。
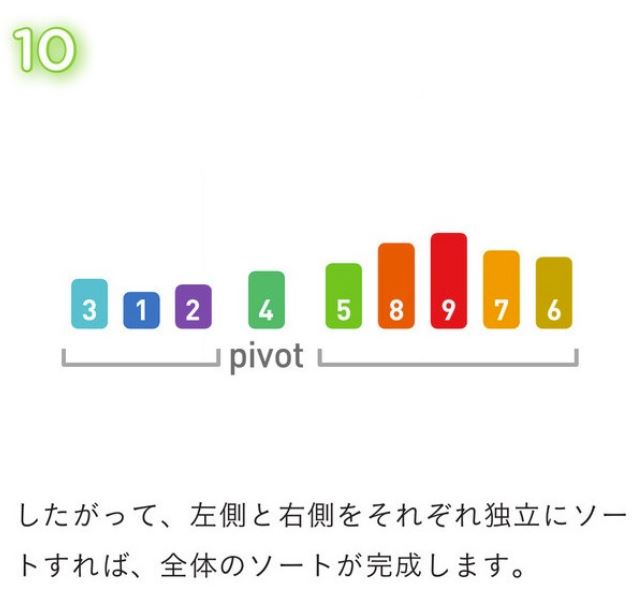
(3)-
二分割された各々のデータを、それぞれ並び替える。
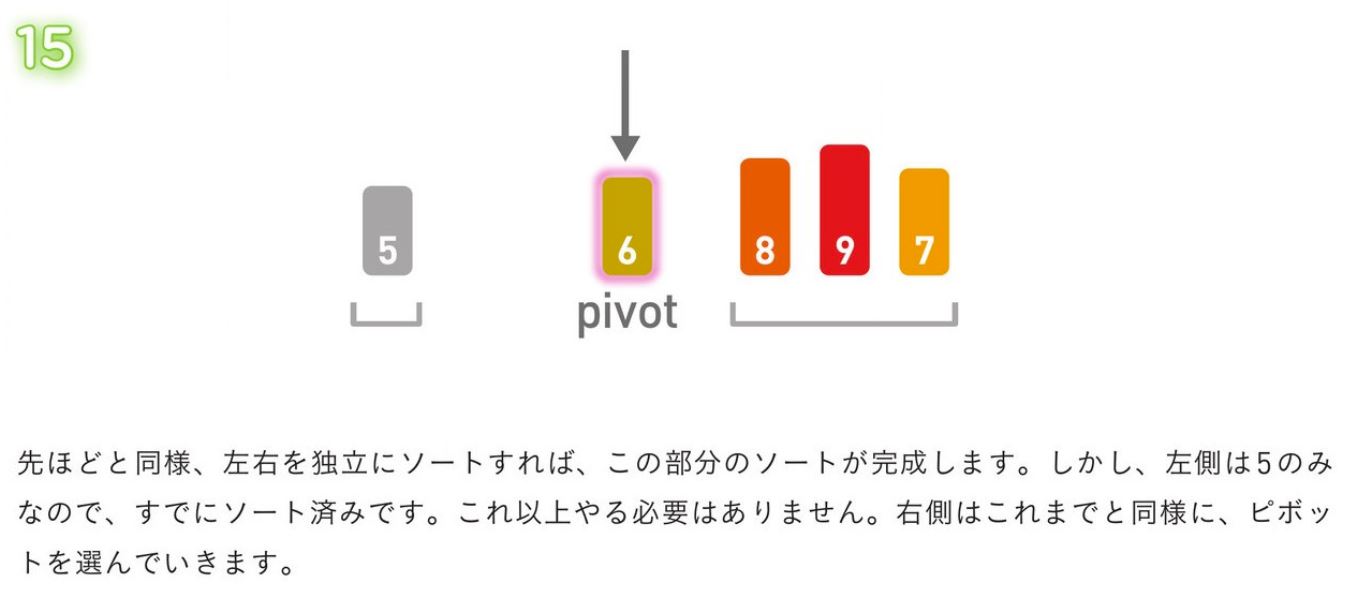
(4)-
ソートを繰り返し実行する。
<?php
function quickSort(array $array): array
{
// 配列の要素数が1つしかない場合、クイックソートする必要がないため、返却する。
if (count($array) <= 1) {
return $array;
}
// 一番最初の値をPivotとする。
$pivot = array_shift($array);
// グループを定義
$left = $right = [];
foreach ($array as $value) {
if ($value < $pivot) {
// Pivotより小さい数は左グループに格納
$left[] = $value;
} else {
// Pivotより大きい数は右グループに格納
$right[] = $value;
}
}
// 処理の周回ごとに、結果の配列を結合。
return array_merge
(
// 左のグループを再帰的にクイックソート。
quickSort($left),
// Pivotを結果に組み込む。
array($pivot),
// 左のグループを再帰的にクイックソート。
quickSort($right)
);
}
<?php
// 実際に使用してみる。
$array = array(6, 4, 3, 7, 8, 5, 2, 9, 1);
$result = quickSort($array);
var_dump($result);
// 昇順に並び替えられている。
// 1, 2, 3, 4, 5, 6, 7, 8
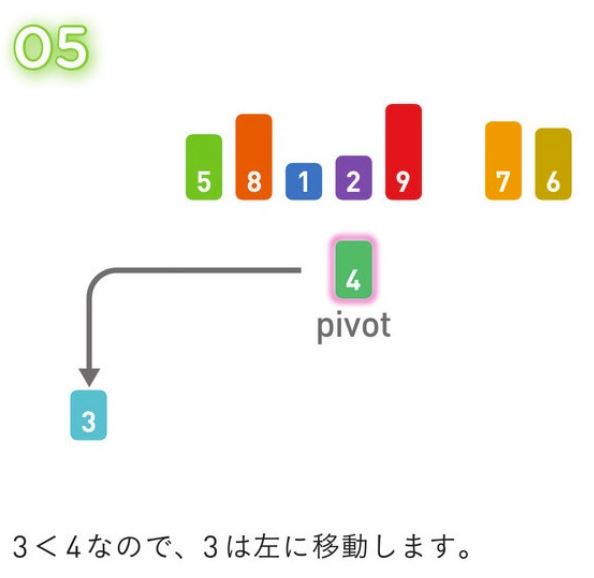
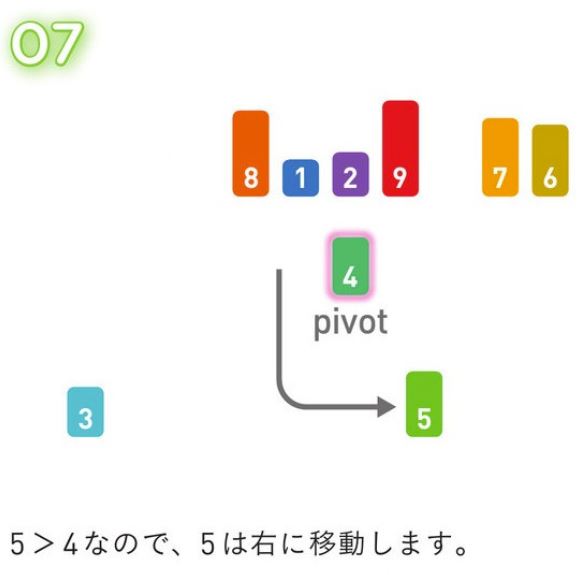
*アルゴリズム解説*
適当な値を基準値 (Pivot) とし、それより小さな値のグループと大きな値のグループに分割する。
同様にして、両グループの中でPivotを選択し、2 個のグループに分割する。
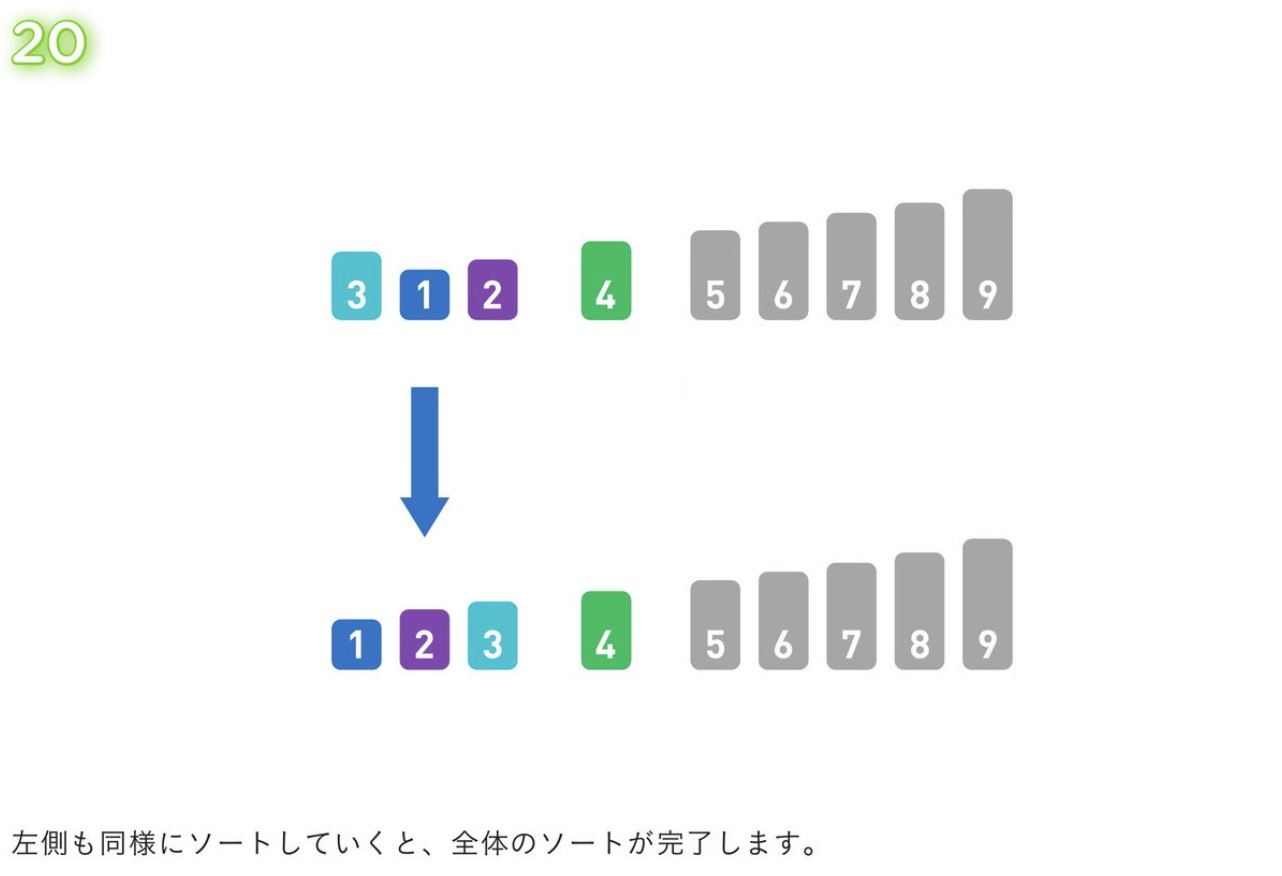
グループ内の値が1つになるまで、この処理を繰り返していく。

















基本交換法 (バブルソート)¶
隣り合ったデータの比較と入替えを繰り返すことによって、小さな値のデータを次第に端のほうに移していく。










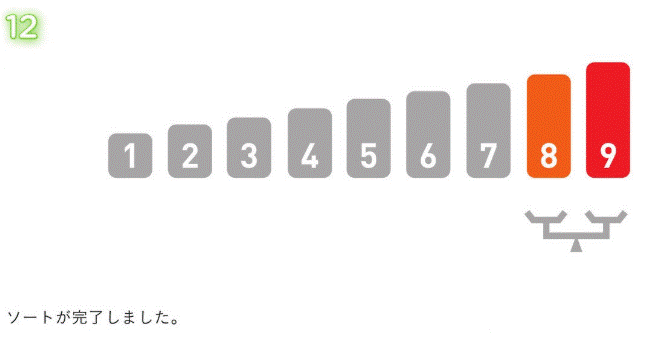
基本挿入法 (挿入ソート)¶
すでに整列済みのデータ列の正しい位置に、データを追加する操作を繰り返していく。
ヒープソート¶
シェルソート¶
02. 配列内探索のアルゴリズム¶
線形探索法¶
今回は、配列内で『6』を探す。


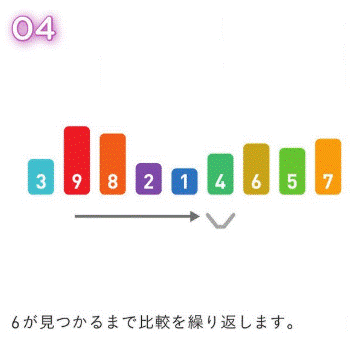


二分探索法¶
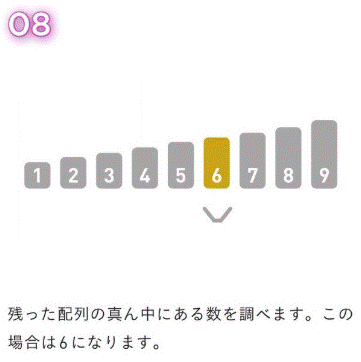
前提として、ソートによって、すでにデータが整列させられているとする。
今回は、配列内で『6』を探す。


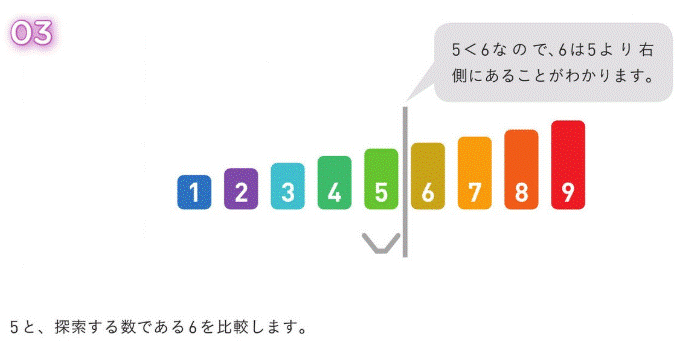

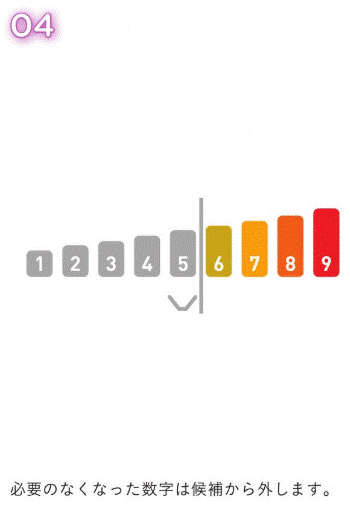

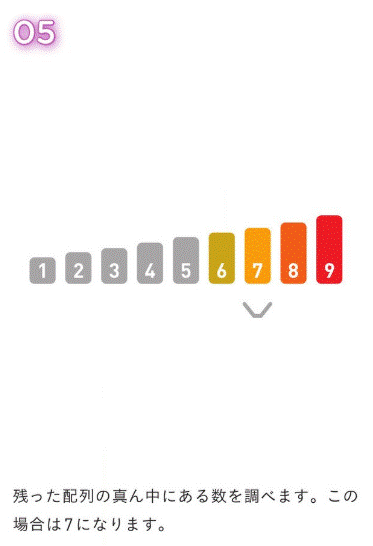

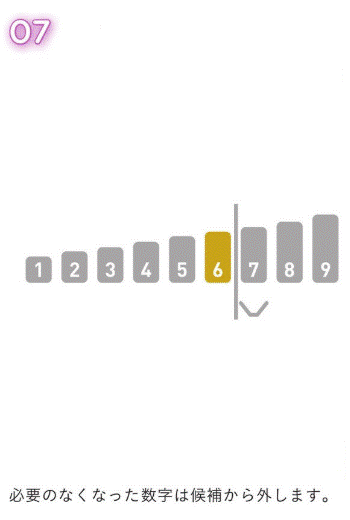

03. グラフ探索のアルゴリズム (難し過ぎで記入途中)¶
ダイクストラ法による最良優先探索¶
*実装例*
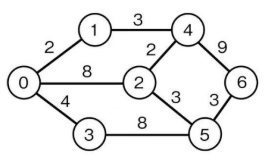

地点間の距離を表で表す。ただし、同地点間の距離は『0』、隣り合わない地点間の距離は『-1』とする。
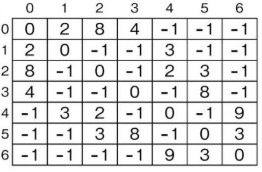

<?php
// 各地点間の距離を二次元の連想配列で定義
$matrix = array(
"P0" => array(0, 2, 8, 4, -1, -1, -1),
"P1" => array(2, 0, -1, -1, 3, -1, -1),
"P2" => array(8, -1, 0, -1, 2, 3, -1),
"P3" => array(4, -1, -1, 0, -1, 8, -1),
"P4" => array(-1, 3, 2, -1, 0, -1, 9),
"P5" => array(-1, -1, 3, 8, -1, 0, 3),
"P6" => array(-1, -1, -1, -1, 9, 3, 0)
);
<?php
// 各地点間の距離、出発地点、開始地点を引数にとる。
function bestFirstSearchByDijkstra(
array $matrix,
int $startPoint,
int $goalPoint
)
{
// 地点数を定数で定義
define("POINT_NUMBER", count($matrix));
if($startPoint < self::POINT_NUMBER
|| self::POINT_NUMBER < $goalPoint){
throw new Exception("存在しない地点番号は設定できません。");
}
// 出発地点を定数で定義
define("START_POINT", $startPoint);
// 到着地点を定数で定義
define("GOAL_POINT", $goalPoint));
// 無限大の定数のINFを使いたいが、定数は上書きできないため、代わりに-1を使用。
// 各頂点に対して、最短ルート地点番号、地点間距離のゼロ値、最短距離確定フラグを設定。
for($i = 0; $i < self::POINT_NUMBER; $i ++){
$route[$i] = -1;
$distance[$i] = -1;
$fixFlg[$i] = false;
}
// *別の書き方*
// $cost = array_fill(0, self::POINT_NUMBER, -1);
// $distance = array_fill(0, self::POINT_NUMBER, -1);
// $fix = array_fill(0, self::POINT_NUMBER, false);
// 出発地点から出発地点への距離をゼロとする。
$distance[self::START_POINT] = 0;
//
while(true){
$i = 0;
while($i < self::POINT_NUMBER){
if(!$fixFlg[$i]){
break 1;
}
$i += 1;
}
if($i === self::POINT_NUMBER){
break 1;
}
for($j = $i + 1; j < self::POINT_NUMBER; $j ++){
if(!$fixFlg[$i] && $distance[$j] < $distance[$i]){
$i = $j;
}
}
// 今の自分には、これ以上は難しい…
// 未来の俺、頑張ってくれ…
}
}
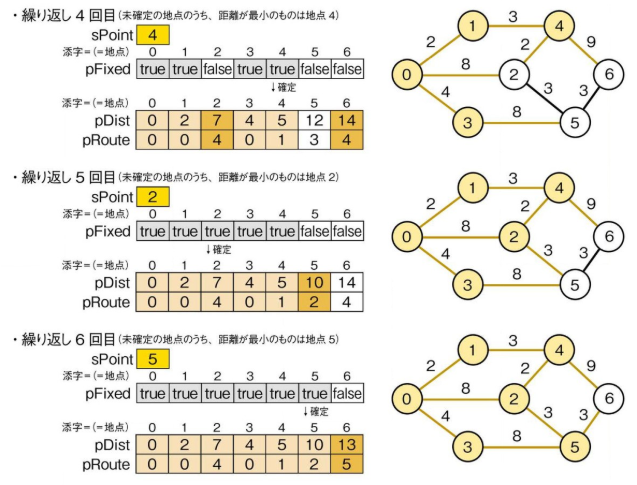
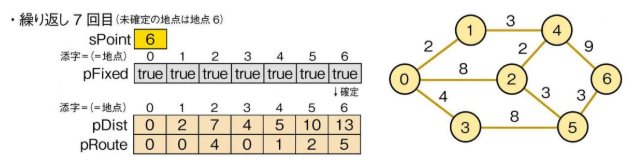
*最短経路探索処理の解説*
$startPoint = 0
$goalPoint = 6
としたとき、出発地点 (0) から1ステップ行ける地点までの距離 (pDist) を取得し、確定させる。
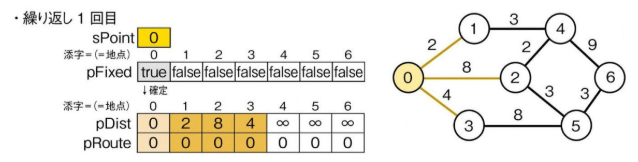
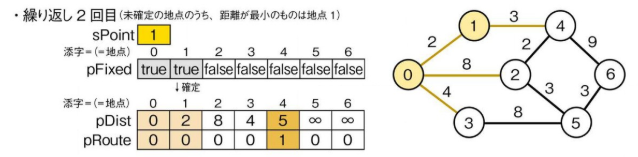
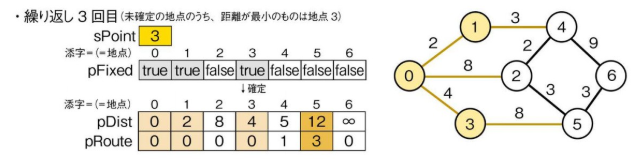
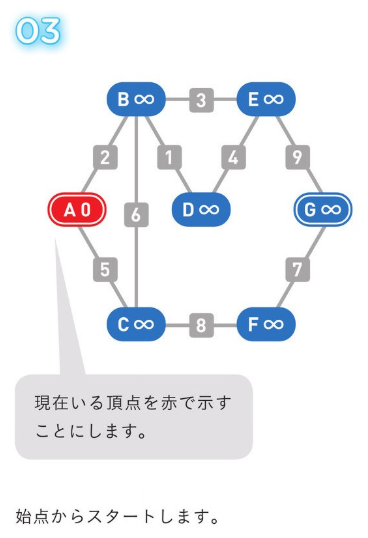
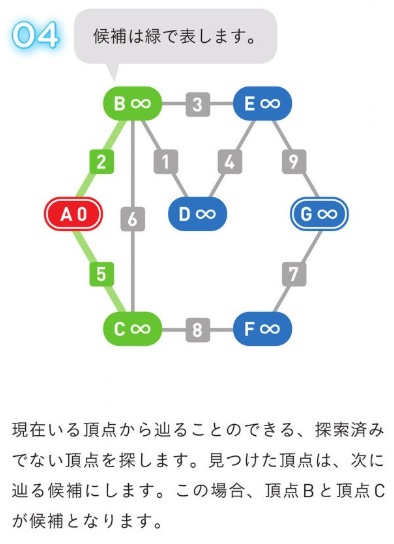
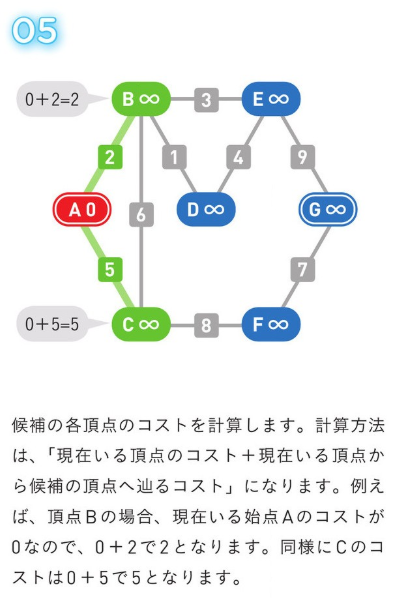
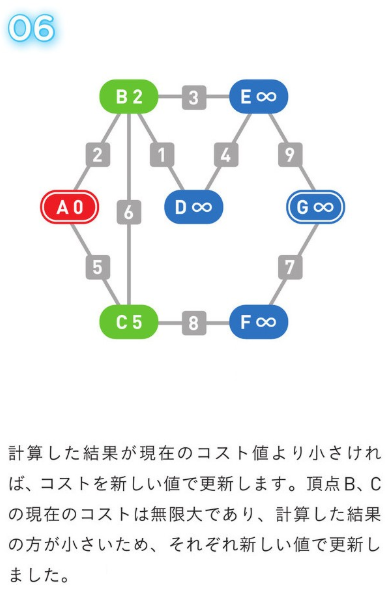
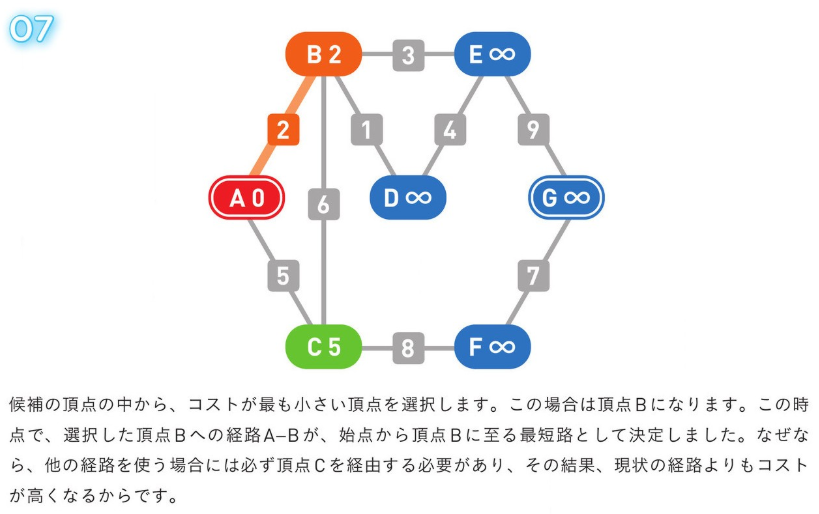
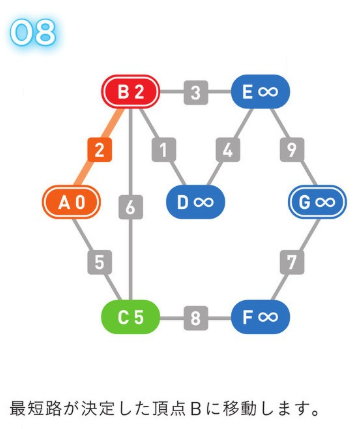
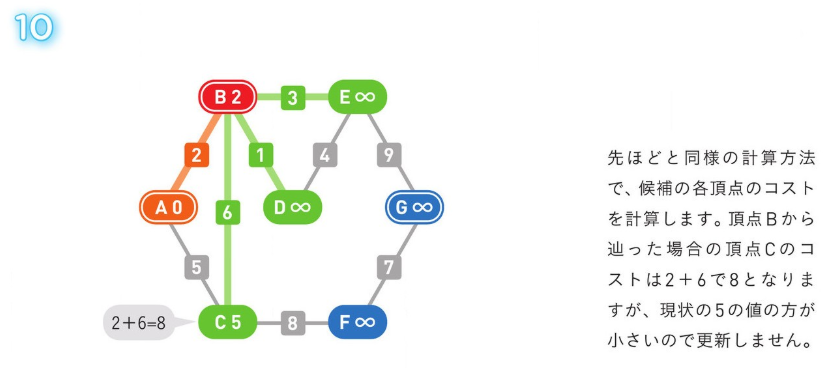
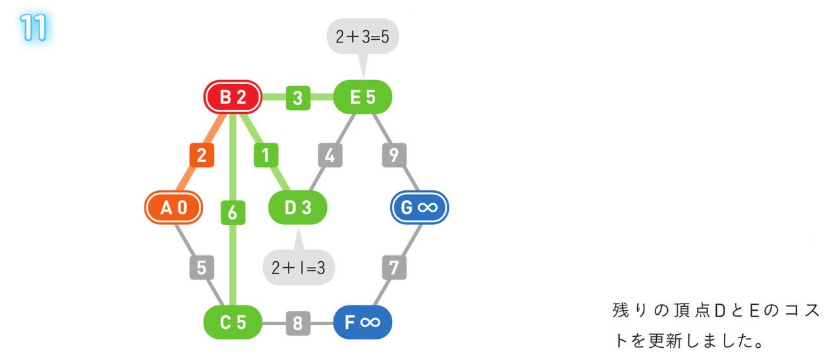
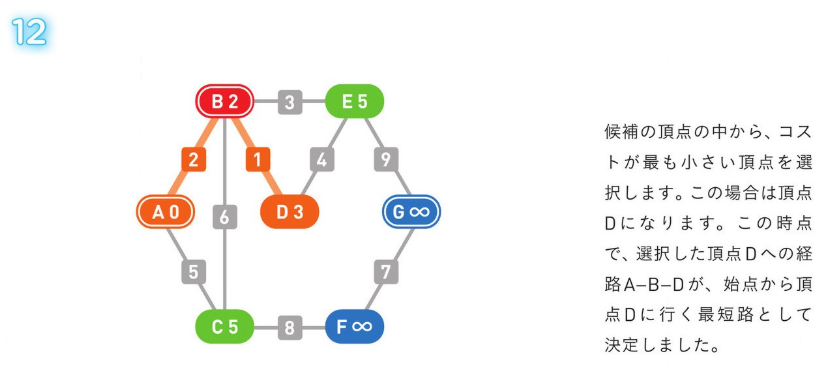
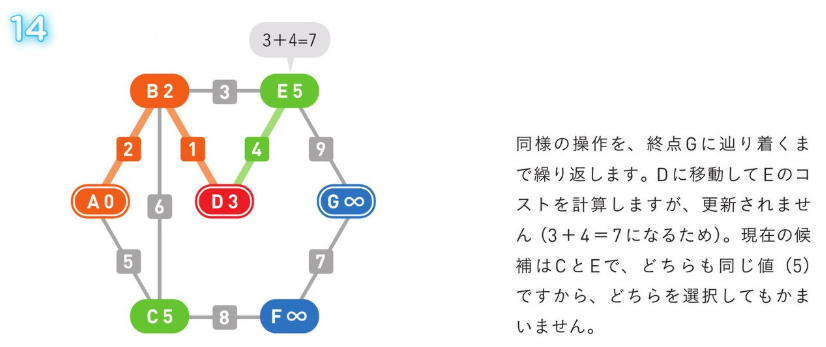
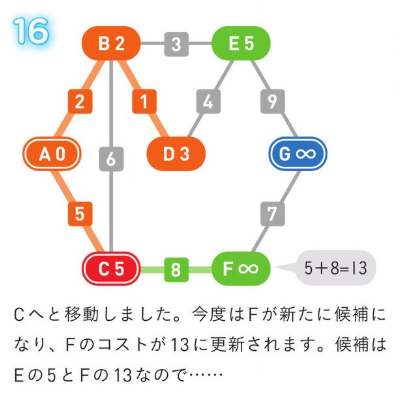
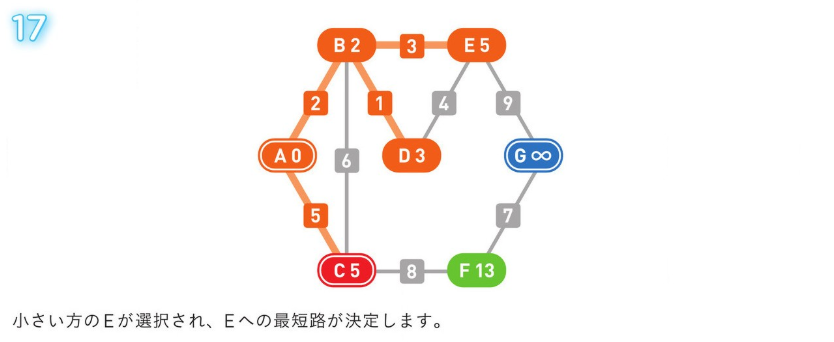
*アルゴリズム解説*
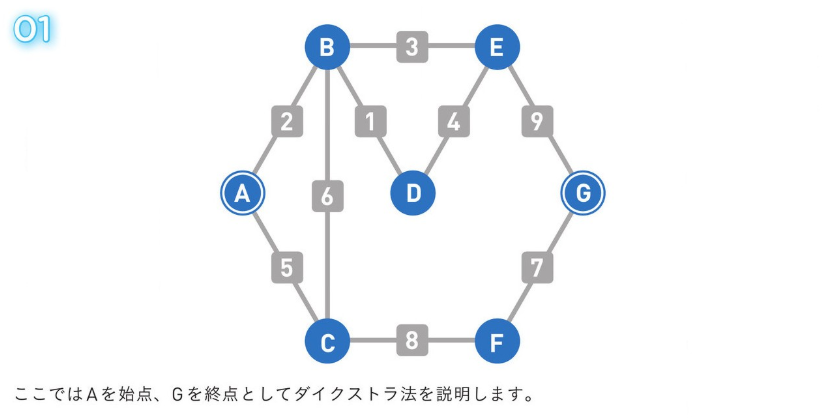
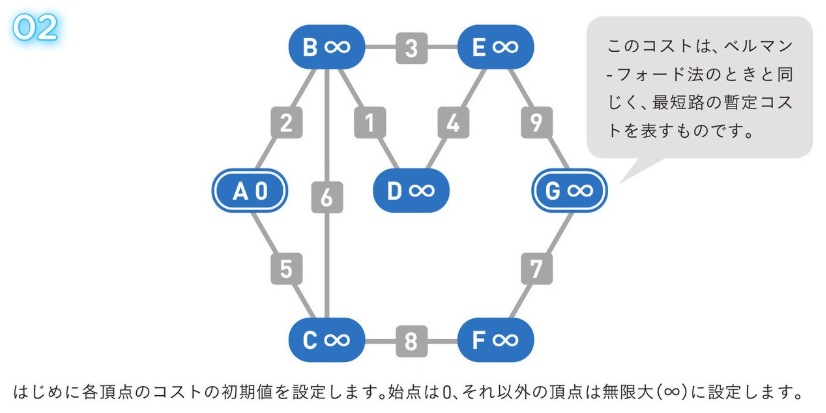
正のコストの経路のみの場合、使用される方法。














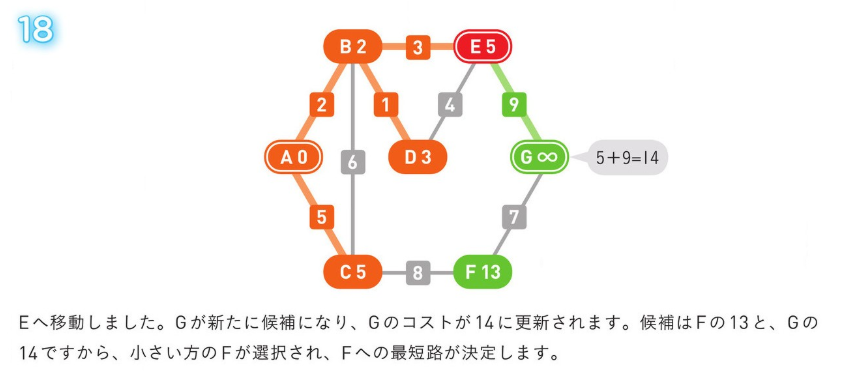

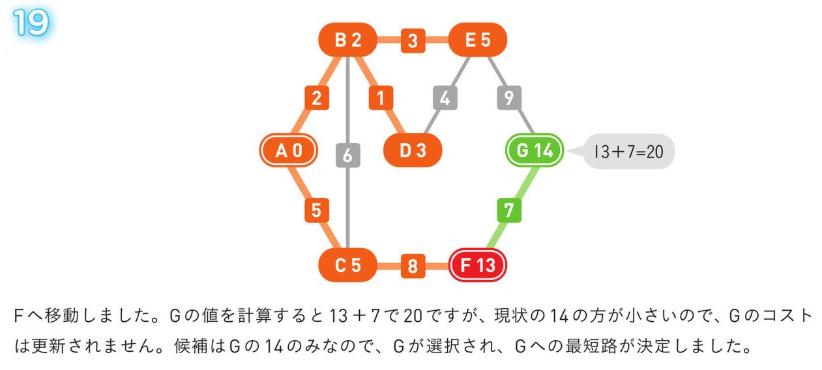

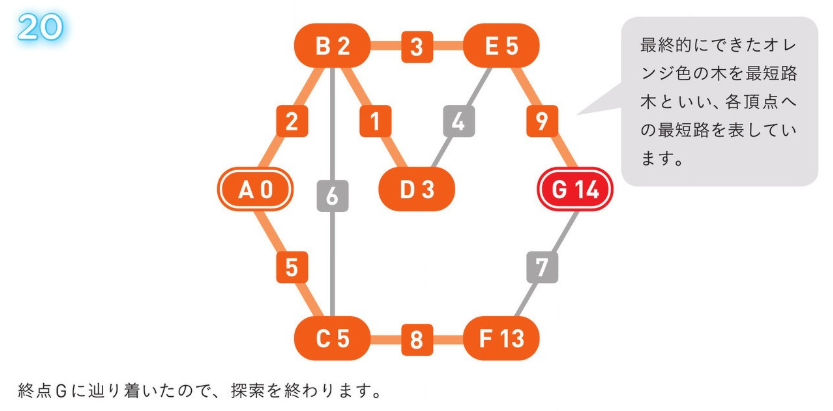
04. 誤り検出と訂正のアルゴリズム¶
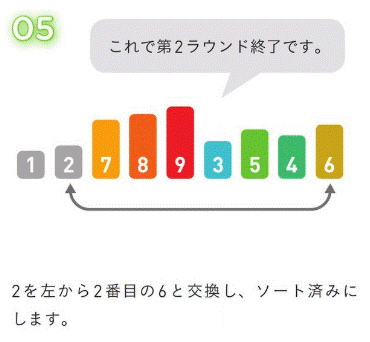
Check Digit Check¶
バーコードやクレジットカードなどの読み取りチェックで使われている誤り検出方法。
(1)-
Check Digitを算出する。
(2)-
算出されたCheck Digitが正しいかを検証する。